新しいフォルダー（１）

メモです。よろしくおねがいします。

[JS] グローバルオブジェクト

グローバルオブジェクト

JavaScript上に存在する組み込みオブジェクトやその他ユーザ定義のオブジェクトは全てオブジェクトに格納されている必要がある.
その格納するオブジェクトの内, 最上位に位置するオブジェクトがグローバルオブジェクトと呼ばれるものである.
全てのJavaScriptの実行環境は必ず１つのグローバルオブジェクトを持たなければならない.
Webブラウザ上で動作するJavaScriptの場合はwindow, Node.jsの場合はglobalがグローバルオブジェクトである.

グローバルオブジェクトは明示的に生成することができない.
つまりnew演算子などを用いてオブジェクトを生成することができないということである.
グローバルオブジェクトはJavaScriptのコードが解釈され, 初期化される際に生成される.

また, グローバルオブジェクトは特別な扱いになっており, グローバルオブジェクトのプロパティへアクセスする場合, グローバルオブジェクトの名前を省略できる.

window.alert('foo')
alert('bar')

また, グローバルオブジェクトを明示しない方が処理速度が僅かに速いため, 後者のように記述するのがベターである.

[暗号] IPとIP^-1

暗号

ITC Advent Calendar ７日目.

今日はDESのIPとIP-1についてです.

誰も興味ないとか知らねーです.

IP

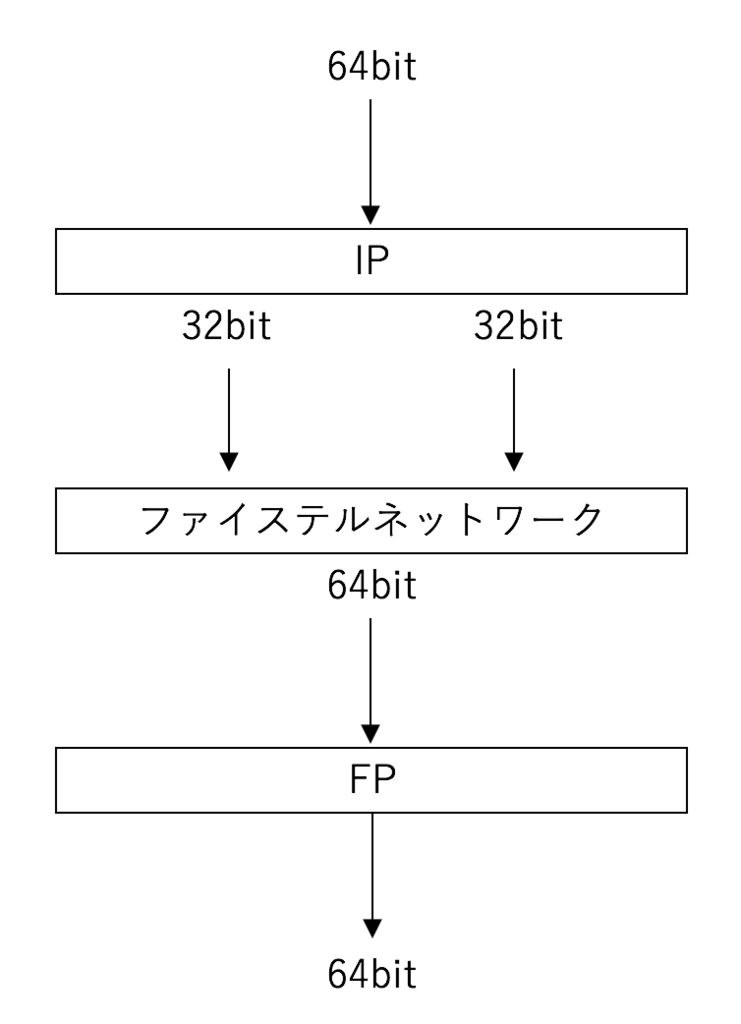
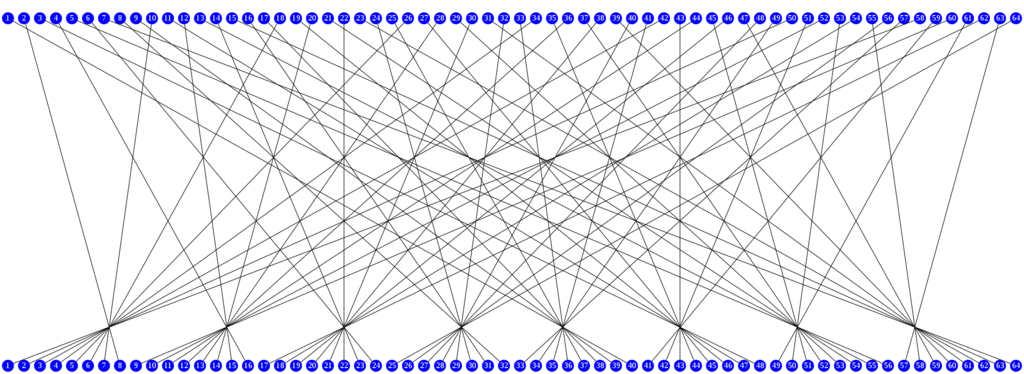
IP(Initial permutation, 初期転置)とは, 入力された64bitの平文に対して最初に行われる転置処理である.

IPには以下のテーブルを用いる.

例えば, 入力された64bitの平文の58bit目が１bit目に転置される.

58 50 42 34 26 18 10 2
60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6
64 56 48 40 32 24 16 8
57 49 41 33 25 17 9 1
59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5
63 55 47 39 31 23 15 7

f:id:Q_tyokinuhata:20171206161413p:plain

DES supplementary material (August. 7, 2017, 08:20 UTC). In Wikipedia: The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/DES_supplementary_material

IPでの処理が行われた後, 上位32bitと下位32bitに分割され, ファイステルネットワークに入力される.

IP-1

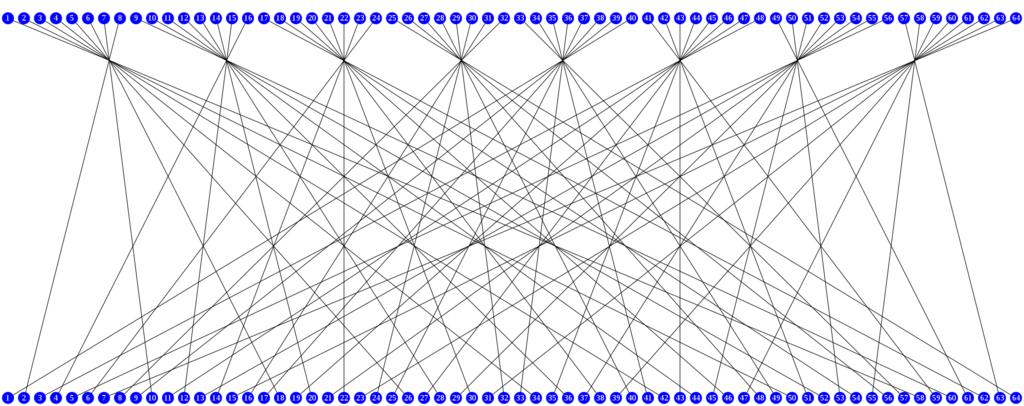
IP-1(Final permutation, 最終転置)とは, ファイステルネットワークから出力された64bitの暗号文に対して行われる転置処理である.

IP-1には以下のテーブルを用いる.

例えば, 入力された64bitの暗号文の40bit目が１bit目に転置される.

40 8 48 16 56 24 64 32
39 7 47 15 55 23 63 31
38 6 46 14 54 22 62 30
37 5 45 13 53 21 61 29
36 4 44 12 52 20 60 28
35 3 43 11 51 19 59 27
34 2 42 10 50 18 58 26
33 1 41 9 49 17 57 25

f:id:Q_tyokinuhata:20171206165428p:plain

DES supplementary material (August. 7, 2017, 08:20 UTC). In Wikipedia: The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/DES_supplementary_material

[暗号] Sボックス

暗号

ITC Advent Calendar ６日目.

今日はSボックスについてです.

誰も興味ないとか知らねーです.

Sボックス

Sボックス(subscription box, S-box)とは, 平文と暗号文の相関(線形性)を壊すための仕組みとして利用される関数のことである.

Sボックスは, mビットの入力をnビットに変換して出力する関数であり, 2mのルックアップテーブルによって実装される.

DESなどの多くのブロック暗号では固定のテーブルが使用されるが, BlowfishやTwofishなどのように鍵によって動的にテーブルが生成されることもある.

1970年代に設計されたDESでは６bitの入力から４bitを出力するSボックスを８種類使用しているが, 2000年代に設計されたAESでは８bit入出力のSボックスを１種類, Camelliaでは８bit入出力のSボックスを４種類(それぞれのSボックスは１つ目のSボックスを単純に変換したもの)使用したものとなっている.

これは, ソフトウェアやハードウェアでの実装時に, スピードだけでなくサイズ縮小も優先させた実装も考慮したためである.

ちなみに, DESのSボックスは設計時にIBMの大型コンピュータを数ヶ月使ったほど難しいと言われている.

これは, DESの基となった暗号であるLuciferのSボックスが弱く, 40個の選択平文で破られたため, DESには差分解読法への耐性を持つことを設計方針にしていたためである.

また, 1980年代末に差分解読法が一般に発表(IBM内ではすでに知られていた), 1990年代前半に線形解読法が発見され, これらの解読法に対して耐性を持つことが安全なSボックスの必要条件と認識された.

証明はされていないが, nビット入出力のSボックスの場合, 2の拡大体GF(2m)での逆変換が差分解読法と線形解読法に対して最も強いテーブルだと考えられている.

このとき, 差分確率及び線形確率は, nが奇数の場合は2-n + 1, 偶数の場合は2-n + 2となる.

AESやCamelliaではそれを線形変換されたものが採用されており, 差分確率及び線形確率は2-6である.

近年では, 実装サイズの縮小を目的に小さいSボックスを複数組み合わせて大きなSボックスを構成する方法が取られることがある.

この場合, 上述したような最善の最大差分確率, 最大線形確率は持たないが, 暗号全体で十分な最大特性差分確率, 最大特性線形確率を持つように設計される.

DESにおけるSボックス

DESの６bit入力４bit出力の８つのSボックスのテーブルを以下に示す.

S1 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
00 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7
01 0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8
10 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0
11 15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13
S2 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
00 15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 10
01 3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5
10 0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 15
11 13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9
S3 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
00 10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8
01 13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 1
10 13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7
11 1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 121
S4 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
00 7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15
01 13 8 11 5 6 15 0 3 4 7 2 12 1 10 14 9
10 10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4
11 3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14
S5 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
00 2 12 4 1 7 10 11 6 8 5 3 15 13 0 14|9
01 14 11 2 12 4 7 13 1 5 0 15 10 3 9 8|6
10 4 2 1 11 10 13 7 8 15 9 12 5 6 3 0|14
11 11 8 12 7 1 14 2 13 6 15 0 9 10 4 5|3
S6 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
00 12 1 10 15 9 2 6 8 0 13 3 4 14 7 5 11
01 10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 8
10 9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6
11 4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13
S7 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
00 4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1
01 13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6
10 1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2
11 6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12
S8 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
00 13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7
01 1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2
10 7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8
11 2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11

例えば, S5に011011が入力された場合, １bit目と６bit目を合わせた01と中間４bitである1101に分割され, テーブル中でそれぞれが交わる9, つまり1001が出力される.

DESの規格が公開された際, Sボックスについての設計方針が公開されなかったため, 設計者だけが知っているバックドアが仕組まれているのではないかという点について多年に渡る研究がなされた.

それにより差分解読法が発見され(IBM内ではすでに知られていた), 線形解読法によるDESの解読実験が成功した1944年になり, ようやくSボックスの設計方針が公開された.

このことから, DESは差分解読法に対する耐性を有するように注意深く設計されていたが, 線形解読法に対しては考慮がされていないということが明らかになった.

[暗号] ラウンド関数

暗号

ITC Advent Calendar ５日目.

今日はDESのラウンド関数についてです.

誰も興味ないとか知らねーです.

ラウンド関数

32bitのビット列と48bitのサブ鍵を入力し, 32bitのビット列を出力する関数である.

１. Expansion function(E)

32bitのビット列を48bitに拡張する.

拡張には以下のテーブルが用いられる.

32 1 2 3 4 5
4 5 6 7 8 9
8 9 10 11 12 13
12 13 14 15 16 17
16 17 18 19 20 21
20 21 22 23 24 25
24 25 26 27 28 29
28 29 30 31 32 1

f:id:Q_tyokinuhata:20171202043636p:plain

DES supplementary material (August. 7, 2017, 08:20 UTC). In Wikipedia: The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/DES_supplementary_material

２. XORを取る

サブ鍵と48bitに拡張されたビット列のXORを取る.

３. Subscription(S)

サブ鍵と48bitに拡張されたビット列のXORから得られたビット列を, ６bitずつに分割し, Sボックス(substitution box, S-box)に入力する.

８つのSボックスは入力された６bitのビット列から４bitのビット列を生成して出力される.

このとき, 非線形な変換が行われ, ルックアップテーブルの形式で出力される.

SボックスがDESの安全の根幹であるため, このプロセスが無い場合, 暗号は線形なものとなり容易に破ることができるようになる.

４. Permutation(P)

Sボックスから出力された32bit(４bit * ８)のビット列に対して固定の並び替えを施す.

並び替えには以下のテーブルが用いられる.

16 7 20 21
29 12 28 17
1 15 23 26
5 18 31 10
2 8 24 14
32 27 3 9
19 13 30 6
22 11 4 25

f:id:Q_tyokinuhata:20171202094310p:plain

DES supplementary material (August. 7, 2017, 08:20 UTC). In Wikipedia: The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/DES_supplementary_material

Eでの拡張とSボックスでの置換, Pでの並び替えが各ラウンドで左側32bitと右側32bitに交互に行われることで, クロード・シャノンが安全で実用的な条件とした「拡散とかく乱」が提供される.

[暗号] 鍵スケジュール

暗号

ITC Advent Calendar ４日目.

今日はDESの鍵スケジュールについてです.

誰も興味ないとか知らねーです.

鍵スケジュール

鍵スケジュールとは, DESなどのブロック暗号において入力された64bitの鍵から48bitのサブ鍵を16個生成する部分である.

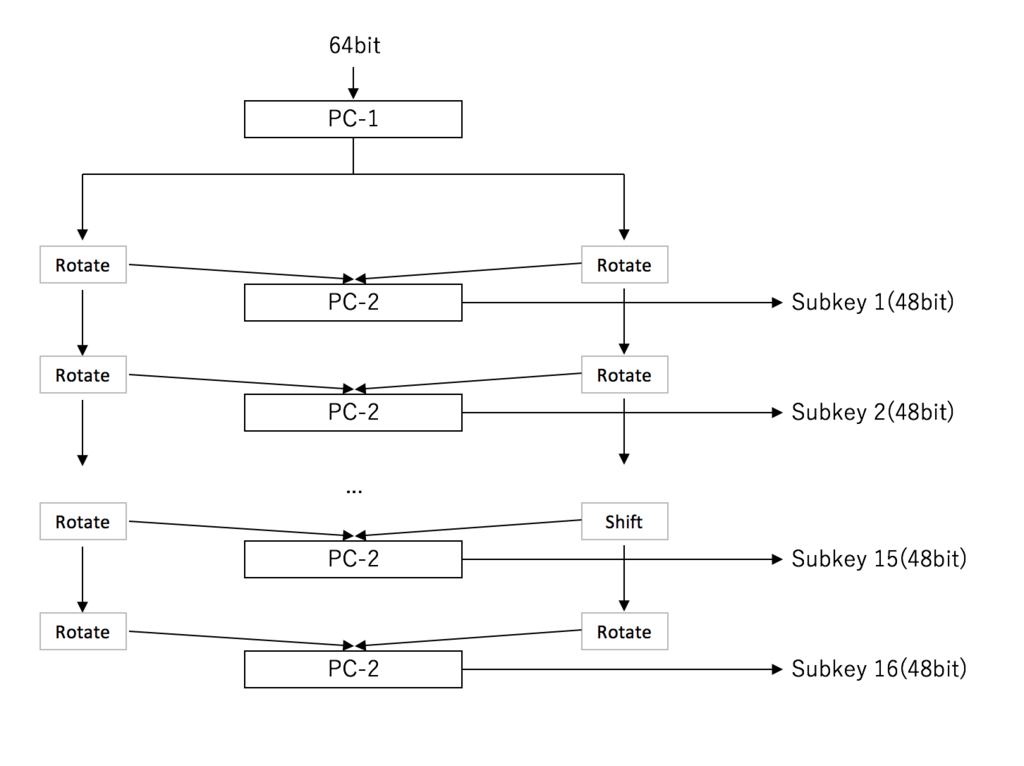
１. Permuted Choice 1(PC-1)

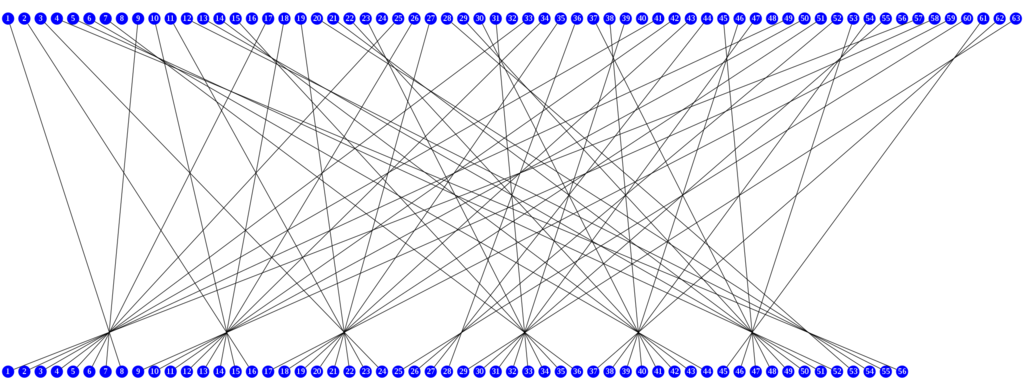
64bitの鍵から56ビットを選択して並べ替えを行う部分をPermuted Choice 1(PC-1)と呼ぶ.

64bitの鍵から56ビット(28ビット * 2)のビット列を生成するには, 以下のテーブルを用いて並び替えを行い, 選択される.

57 49 41 33 25 17 9
1 58 50 42 34 26 18
10 2 59 51 43 35 27
19 11 3 60 52 44 36
63 55 47 39 31 23 15
7 62 54 46 38 30 22
14 6 61 53 45 37 29
21 13 5 28 20 12 4

f:id:Q_tyokinuhata:20171202021829p:plain

DES supplementary material (August. 7, 2017, 08:20 UTC). In Wikipedia: The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/DES_supplementary_material

例えば１bit目は８番目に移動され, ２bit目は16番目に移動される.

選ばれなかった８bitは捨てても良いし, パリティビットとして鍵のチェックに使用しても良い.

また, 選択された56bitは28ビットずつに分割され, ラウンドを１つ進めるごとに１bitか２bitローテートされる.

これはラウンドによってローテートされるbit数が異なり, ラウンドとローテートされるbit数は以下のように対応している.

ラウンド bit数
１ １
２ １
３ ２
４ ２
５ ２
６ ２
７ ２
８ ２
９ １
10 ２
11 ２
12 ２
13 ２
14 ２
15 ２
16 １

２. Permuted Choice 2(PC-2)

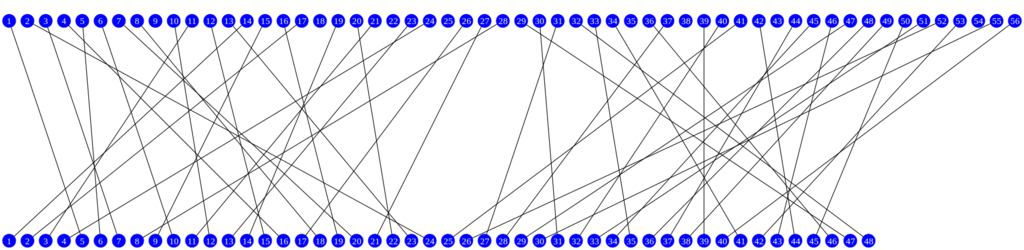
Permuted Choice 2(PC-2)には, PC-1で生成された28bitのビット列をが入力される.

28bitのビット列からそれぞれ24bitずつ選択し, 並び替えもそれぞれ行う.

PC-2自体は固定であり, 毎回同じ位置のビットを選択し, 同じ順序で並び替え, ２つのビット列を結合することで48bitのサブ鍵が得られる.

各ビットは16ラウンドのうち, だいたい14回程度使用される.

14 17 11 24 1 5
3 28 15 6 21 10
23 19 12 4 26 8
16 7 27 20 13 2
41 52 31 37 47 55
30 40 51 45 33 48
44 49 39 56 34 53
46 42 50 36 29 32

f:id:Q_tyokinuhata:20171202023935p:plain

DES supplementary material (August. 7, 2017, 08:20 UTC). In Wikipedia: The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/DES_supplementary_material

上述したローテートとPC-2の処理がラウンドごと(つまり16回)行われ, サブ鍵が生成される.

[暗号] ファイステルネットワーク

暗号

ITC Advent Calendar ３日目.

今日から数日間に分けてブロック暗号の構造を解説します.

今日はファイステルネットワークについてです.

誰も興味ないとか知らねーです.

ファイステルネットワーク

ファイステルネットワークはファイステル構造, ファイステル暗号とも呼ばれ, ブロック暗号の構造の一種である.

殆どのブロック暗号は, 実装コストを効率化するために同一のラウンドを繰り返すようになっており, ファイステルネットワークはそれを実現する代表的な構造である.

他の構造としては, SPN構造がある.

1977年にIBMのホルスト・ファイステル(Horst Feistel)が開発したDESに基本構造として使われていたことからこう呼ばれている.

DES以降, FEAL, MISTY1, Camelliaなど, 多くのブロック暗号でこの構造が採用されている.

ラウンド

ファイステルネットワークでは, ラウンドと呼ばれる暗号化の１ステップを何度も繰り返すようになっており, 下図はファイステル構造における１ラウンドを図式化したものである.

なお, DES(ブロック長: 64bit)を例としている.

K: サブ鍵. 鍵スケジュールにより, 入力された64bit長の鍵から48bit長のサブ鍵が16個生成される.

F: ラウンド関数. 右側32bitとサブ鍵を元に左側32bitを暗号化するためのビット列を生成する関数.

１. 入力された平文(64bit)を２等分し, 32bitずつに分割する.

２. 右側32bitとサブ鍵をラウンド関数Fに入力し, 32bitのビット列を生成する.

３. ラウンド関数Fから出力された32bitのビット列と左側32bitのXORを取る.

これで１ラウンドとする.

なお, 暗号化された左側32bitは次のラウンドの右側32bitの入力, 暗号化されていない右側32bitは次のラウンドの左側32bitの入力となる.

ラウンドは16回繰り返され, その度に左側と右側が交換されるが, 最終ラウンドの後では交換を行わない.

また, 暗号化と復号が全く同じ構造で実現できるのがファイステルネットワークの特徴である.

ファイステルネットワークにおける１ラウンドでは, 右側32bitに対して何の処理も行わないため一見無駄に見えるが, これにより復号が保証されることになる.

入れ子型構造

MISTYでは, ラウンド関数の内部にさらにファイステルネットワークを組み込んでおり, これを入れ子型構造と呼ぶ.

MISTYでは３段階の入れ子型構造を取っており, これは差分解読法や線形解読法などの暗号解読法に対する証明可能安全性を実現し, 規模の削減にも効果がある.

変形ファイステルネットワーク

MARSでは, 入力を４分割し, それぞれの間で処理を行うような構造となっている.

一般的にn(n > 2)分割するファイステルネットワークを変形ファイステルネットワークと呼ぶ.

ブロック暗号のブロック長が大きい場合にラウンド関数のビット幅を小さくすることができる.

[文字コード] Base64

文字コード

Base64

データを64種類の英数字を用い, それ以外の文字を扱うことのできない環境にてマルチバイト文字やバイナリデータを扱うためのエンコーディング方式である.

RFC 2045の6.8項で定義されている.

使用できる文字は, A - Z, a - z, 0 - 9, +, /の64文字とパディング用の記号=の計65文字である.

MIMEによって規定されており, ７ビットのデータしか扱うことのできない電子メールにて広く利用されている.

Base64で変換されたデータは元データの4/3(約133%)となる.

また, MIMEでは76文字毎に改行コードが入る仕様のため, この２バイト分を含めると元データの約137%となる.

生まれた経緯

現在では拡張機能により８bit以上のマルチバイト文字やバイナリデータも送ることが可能だが, かつてはASCII文字で表現できる文字しか送ることができなかった.

そこで, メール上で様々なフォーマットを扱えるようにするMIME(Multipurpose Internet Mail Extensions)という規格が規定され, その中でBase64というエンコーディング方式が定義された.

今日では, JSONで特殊文字を含まないように画像データをエンコードしたり, Webページを表示する際にリクエスト数を減らすためにBase64でエンコードした画像をHTMLに埋め込むなどの用途で用いられている.

変換表

数値と文字の対応を以下に示す.

10進数 ２進数 文字 10進数 ２進数 文字 10進数 ２進数 文字 10進数 ２進数 文字
0 000000 A 16 010000 Q 32 100000 g 48 110000 w
1 000001 B 17 010001 R 33 100001 h 49 110001 x
2 000010 C 18 010010 S 34 100010 i 50 110010 y
3 000011 D 19 010011 T 35 100011 j 51 110011 z
4 000100 E 20 010100 U 36 100100 k 52 110100 0
5 000101 F 21 010101 V 37 100101 l 53 110101 1
6 000110 G 22 010110 W 38 100110 m 54 110110 2
7 000111 H 23 010111 X 39 100111 n 55 110111 3
8 001000 I 24 011000 Y 40 101000 o 56 111000 4
9 001001 J 25 011001 Z 41 101001 p 57 111001 5
10 001010 K 26 011010 a 42 101010 q 58 111010 6
11 001011 L 27 011011 b 43 101011 r 59 111011 7
12 001100 M 28 011100 c 44 101100 s 60 111100 8
13 001101 N 29 011101 d 45 101101 t 61 111101 9
14 001110 O 30 011110 e 46 101110 u 62 111110 +
15 001111 P 31 011111 f 47 101111 v 63 111111 /

変換アルゴリズム

文字列ABCDEFGを例にエンコードを行う.

１. ２進数に変換

元データ 16進数表現 ２進数表現
A 0041 01000001
B 0042 01000010
C 0043 01000011
D 0044 01000100
E +0045 01000101
F 0046 01000110
G 0047 01000111

２. ６bitずつに分割

010000 010100 001001 000011 010001 000100 010101 000110 010001 11

３. ゼロパディング

最後の２bitが余っているので, 0でパディングする.

010000 010100 001001 000011 010001 000100 010101 000110 010001 110000

４. 文字に変換

変換表を参考に４文字ずつ変換する.

QUJD REVG Rw

５. パディング

２文字余っているので, =でパディングする.

QUJD REVG Rw==

６. 繋げる

QUJDREVGRw==

Python3による実装

変換表(JSON形式)

{
    "000000": "A",
    "000001": "B",
    "000010": "C",
    "000011": "D",
    "000100": "E",
    "000101": "F",
    "000110": "G",
    "000111": "H",
    "001000": "I",
    "001001": "J",
    "001010": "K",
    "001011": "L",
    "001100": "M",
    "001101": "N",
    "001110": "O",
    "001111": "P",
    "010000": "Q",
    "010001": "R",
    "010010": "S",
    "010011": "T",
    "010100": "U",
    "010101": "V",
    "010110": "W",
    "010111": "X",
    "011000": "Y",
    "011001": "Z",
    "011010": "a",
    "011011": "b",
    "011100": "c",
    "011101": "d",
    "011110": "e",
    "011111": "f",
    "100000": "g",
    "100001": "h",
    "100010": "i",
    "100011": "j",
    "100100": "k",
    "100101": "l",
    "100110": "m",
    "100111": "n",
    "101000": "o",
    "101001": "p",
    "101010": "q",
    "101011": "r",
    "101100": "s",
    "101101": "t",
    "101110": "u",
    "101111": "v",
    "110000": "w",
    "110001": "x",
    "110010": "y",
    "110011": "z",
    "110100": "0",
    "110101": "1",
    "110110": "2",
    "110111": "3",
    "111000": "4",
    "111001": "5",
    "111010": "6",
    "111011": "7",
    "111100": "8",
    "111101": "9",
    "111110": "+",
    "111111": "/"
}

Base64(Python3)

#!/usr/bin/env python

import sys
import json

# ２進数に変換
def str_to_bin(str):
    bin = ''
    for char in str:
        bin += format(ord(char), 'b').zfill(8)
    return bin

# ６bitずつに分割
def split(bin, split_cnt):
    split_bin = [bin[i: i + split_cnt] for i in range(0, len(bin), split_cnt)]
    return split_bin

# ゼロパディング
def zero_padding(split_bin, padding_interval):
    for i in range(padding_interval - 1):
        if len(split_bin) >= padding_interval:
            break
        split_bin += '0'
    return split_bin

# '='でパディング
def equal_padding(base64, padding_interval):
    padding_num = len(base64) % padding_interval
    for i in range(padding_num):
        base64 += '='
    return base64

def main():
    # コマンドライン引数を受け取る
    argvs = sys.argv
    argc = len(argvs)

    # 引数が１つでなければ処理を行わず終了
    if argc != 2:
        print('usage: python %s STRING' %argvs[0])
        sys.exit()

    # ２進数に変換
    bin = str_to_bin(argvs[1])

    # ６bitずつに分割
    split_cnt = 6
    split_bin = split(bin, split_cnt)

    # ゼロパディング
    split_bin[-1] = zero_padding(split_bin[-1], 6)

    # 変換表の読み込み
    base64_table = json.loads(open('base64_table.json', 'r').read())

    # 文字に変換
    base64 = ''
    for i in split_bin:
        base64 += base64_table[i]

    # '='でパディング
    base64 = equal_padding(base64, 4)

    # 出力
    print(base64)

if __name__ == '__main__':
    main()

実行

$ python base64.py ABCDEFG

実行結果

QUJDREVGRw==